Value & Capital, CHAPTER V, Section 2

Hicks begins his examination of the stability of equilibrium with the case of simple exchange of two goods, X and Y.  In this case, the equilibrium condition is that supply equals demand for one of the goods (as this implies that supply equals demand for the other good as well).  The stability condition for equilibrium is that "a fall in the price of X in terms of Y will make the demand for X greater than the supply of X."  Hicks defines the excess demand as the difference between demand and supply at each price.  Given this definition, the equilibrium condition is that excess demand must equal zero, and the stability condition is that a fall in price should increase the excess demand (since it must become positive, after having been zero).  Hicks plots supply, demand, and excess demand curves together on Figure 14.

Hicks states that it is "obvious" from this diagram that "when the demand curve slopes downward to the right, and the supply curve upwards to the right, the excess demand curve must be downward sloping."  Just in case this doesn't seem obvious, note that on this diagram the demand curve is a line with negative slope, and the supply curve is a line with positive slope, therefore demand minus supply must be a line with negative slope.  (Note also that this figure, like most in economics, plots price on the vertical axis, so we read the quantity for a given price horizontally -- hence the price level at which the excess demand curve crosses the price axis is exactly the price level at which supply equals demand.)

Hicks then asks what can be said in general about the effect of a fall in price on excess demand.

As seen in Chapter II, both supply and demand effects can be analyzed in terms of income and substitution effects;  thus, Hicks argues, excess demand can be analyzed this way as well.  The substitution effect of a fall in price will work to increase demand and reduce supply;  thus the fall in price will tend to increase excess demand.  The income effect works by making buyers better off and sellers worse off.  If the good in question is not an inferior good, this will tend to increase both demand and supply.  Then, as Hicks concludes, "the direction of the income effect on excess demand depends on which of these two tendencies is the stronger."  These income effects could cancel each other out entirely, in which case the excess demand curve will slope downward, and the equilibrium will be stable.  In general, however, there will be some net increase or decrease in excess demand due to the redistribution of income between the buyers and sellers.  Because there will likely be some cancellation in effects, however, Hicks recommends that, "when dealing with problems of the stability of exchange, it is a reasonable method of approach to begin by assuming that income effects do cancel out, and then to inquire what difference it makes if there is a net income effect in one direction or the other."

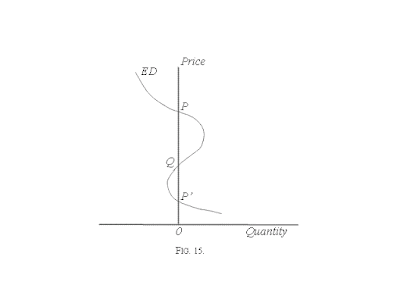
Hicks points out that the equilibrium will still be stable if the net income effect goes in the same direction as the substitution effect.  He notes that the only possibility for instability comes "when there is a strong income effect in the opposite direction -- that is to say, the sellers of X will have to be much more anxious to consume more X when they become better off than the buyers of X are."   He illustrates such a case using Figure 15, in which point Q is unstable.  Even here, however, he notes that this excess demand curve "would still be able to turn round and produce stable positions (such as P or P')."

Hicks points out that the difficulty in a situation such as the one illustrated here is that there may be more than one stable equilibrium.  A change in the tastes of consumers may move the excess demand curve to the right, which in the case of starting from the equilibrium of P', could result in a sharp and discontinuous jump to the new equilibrium position of P.